nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals x
where n is the degree of the root. A root of degree 2 is usually called a square root and a root of degree 3, a cube root.
For example:
- 2 is a square root of 4, since 22 = 4.
- −2 is also a square root of 4, since (−2)2 = 4.
A number may have many roots of degree n and the roots are not necessarily real numbers.
Roots are usually written using the radical symbol 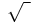 , with
, with  denoting the square root,
denoting the square root, ![\sqrt[3]{x}\!\,](/2012-wikipedia_en_all_nopic_01_2012/I/d466b33802795a4c6e1d9cb930903866.png) denoting the cube root,
denoting the cube root, ![\sqrt[4]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/dc3b0133777287c898c319e89db2c134.png) denoting the fourth root, and so on. In the expression
denoting the fourth root, and so on. In the expression ![\sqrt[n]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/5e4352778f3b156f05ef056f9793ec36.png) , n is called the index,
, n is called the index, 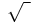 is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a function, so a non-negative real root, called the principal nth root, is preferred rather than others. An unresolved root, especially one using the radical symbol, is often referred to as a surd[1] or a radical.[2] Any expression containing a radical, whether it is a square root, a cube root, or a higher root, is called a radical expression.
is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a function, so a non-negative real root, called the principal nth root, is preferred rather than others. An unresolved root, especially one using the radical symbol, is often referred to as a surd[1] or a radical.[2] Any expression containing a radical, whether it is a square root, a cube root, or a higher root, is called a radical expression.
In calculus, roots are treated as special cases of exponentiation, where the exponent is a fraction:
Roots are particularly important in the theory of infinite series; the root test determines the radius of convergence of a power series. Nth roots can also be defined for complex numbers, and the complex roots of 1 (the roots of unity) play an important role in higher mathematics. Galois theory can be used to determine which algebraic numbers can be expressed using roots, and to prove the Abel-Ruffini theorem, which states that a general polynomial equation of degree five or higher cannot be solved using roots alone; this result is also known as "the insolubility of the quintic".
Contents |
History
The origin of the root symbol √ is largely speculative. Some sources imply that the symbol was first used by Arabic mathematicians. One of those mathematicians was Abū al-Hasan ibn Alī al-Qalasādī (1421–1486). Legend has it that it was taken from the Arabic letter ج, which is the first letter in the word Jadhir "root" in Arabic. (The dh in Jadhir is a voiced interdental fricative, like the th in English the.) Many scholars, however, including Leonhard Euler [3] believe it originates from the letter r, the first letter of radix "root" in Latin word referring to the same mathematical operation. The symbol was first seen in print without the vinculum (the horizontal "bar" over the numbers inside the radical symbol) in the year 1525 in Die Coss by Christoff Rudolff, a German mathematician.
The term surd traces back to al-Khwārizmī (c. 825), who referred to rational and irrational numbers as audible and inaudible, respectively. This later led to the Arabic asamm (deaf, dumb) for irrational number being translated as surdus (deaf or mute) into Latin. Gherardo of Cremona (c. 1150), Fibonacci (1202) and then Robert Recorde (1551) all used the term to refer to unresolved irrational roots.[4]
Definition and notation
The nth root of a number x, where n is a positive integer, is a number r whose nth power is x:
Every positive real number x has a single positive nth root, which is written ![\sqrt[n]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/5e4352778f3b156f05ef056f9793ec36.png) . For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiation as x1/n.
. For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiation as x1/n.
For even values of n, positive numbers also have a negative nth root, while negative numbers do not have a real nth root. For odd values of n, every negative number x has a real negative nth root. For example, −2 has a real 5th root, ![\sqrt[5]{-2} \,= -1.148698354\ldots](/2012-wikipedia_en_all_nopic_01_2012/I/e75bbbba9b8964e457e4a7c0a685487e.png) but −2 does not have any real 6th roots.
but −2 does not have any real 6th roots.
Every non-zero number x, real or complex, has n different complex number nth roots including any positive or negative roots, see complex roots below. The nth root of 0 is 0.
For most numbers, an nth root is irrational. For example,
All nth roots of integers, or in fact of any algebraic number, are algebraic.
For the extension of powers and roots to indices that are not positive integers, see exponentiation.
The character codes for the radical symbols are
| Read | Character | Unicode | ASCII | URL | HTML (others) |
|---|---|---|---|---|---|
| Square root | √ | U+221A | √ |
%E2%88%9A |
√ |
| Cube root | ∛ | U+221B | ∛ |
%E2%88%9B |
|
| Fourth root | ∜ | U+221C | ∜ |
%E2%88%9C |
Square roots
The square root of a number x is that number r which, when squared, becomes x:
Every positive real number has two square roots, one positive and one negative. For example, the two square roots of 25 are 5 and −5. The positive square root is also known as the principal square root, and is denoted with a radical sign:
Since the square of every real number is a positive real number, negative numbers do not have real square roots. However, every negative number has two imaginary square roots. For example, the square roots of −25 are 5i and −5i, where i represents a square root of −1.
Cube roots
A cube root of a number x is a number r whose cube is x:
Every real number x has exactly one real cube root, written ![\sqrt[3]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/a10c7f2aa138b1565920d17c22062a35.png) . For example,
. For example,
Every real number has two additional complex cube roots (see complex roots below).
Identities and properties
Every positive real number has a positive nth root and the rules for operations with such surds are straightforward:
Using the exponent form as in 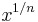 normally makes it easier to cancel out powers and roots.
normally makes it easier to cancel out powers and roots.
Problems can occur when taking the nth roots of negative or complex numbers. For instance:
whereas
when taking the principal value of the roots. See failure of power and logarithm identities in the exponentiation article for more details.
Simplified form of a radical expression
A radical expression is said to be in simplified form if[5]
- There is no factor of the radicand that can be written as a power greater than or equal to the index.
- There are no fractions under the radical sign.
- There are no radicals in the denominator.
For example, to write the radical expression 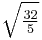 in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it:
in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it:
Next, there is a fraction under the radical sign, which we change as follows:
Finally, we remove the radical from the denominator as follows:
When there is a denominator involving surds it may be possible to find a factor to multiply both numerator and denominator by to simplify the expression. For instance using the factorization of the sum of two cubes:
Simplifying radical expressions involving nested radicals can be quite difficult. It is not immediately obvious for instance that:
Infinite series
The radical or root may be represented by the infinite series:
with 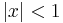 . This expression can be derived from the binomial series.
. This expression can be derived from the binomial series.
Computing principal roots
The nth root of an integer is not always an integer or rational number. For instance, the fifth root of 34 is
The nth root of a number A can be computed by the nth root algorithm, a special case of Newton's method. Start with an initial guess x0 and then iterate using the recurrence relation
until the desired precision is reached.
Depending on the application, it may be enough to use only the first Newton approximant:
For example, to find the fifth root of 34, note that 25 = 32 and thus take x = 32 and y = 2 in the above formula. This yields
The error in the approximation is only about 0.03 %.
Newton's method can be extended to produce a generalized continued fraction for the nth root which can be modified in various ways as described in that article. For example:
![\sqrt[n]{z^m} = \sqrt[n]{(x^n%2By)^m} = x^m%2B\cfrac{my} {nx^{n-m}%2B\cfrac{(n-m)y} {2x^m%2B\cfrac{(n%2Bm)y} {3nx^{n-m}%2B\cfrac{(2n-m)y} {2x^m%2B\cfrac{(2n%2Bm)y} {5nx^{n-m}%2B\cfrac{(3n-m)y} {2x^m%2B\ddots}}}}}};](/2012-wikipedia_en_all_nopic_01_2012/I/032a1ffc66be2ecff1e5925a32b1ff92.png)
![\sqrt[n]{z^m}=x^m%2B\cfrac{2x^m\cdot my}{n(2z - y)-my-\cfrac{(1^2n^2-m^2)y^2}{3n(2z - y)-\cfrac{(2^2n^2-m^2)y^2}{5n(2z - y)-\cfrac{(3^2n^2-m^2)y^2}{7n(2z - y)-\ddots}}}}.](/2012-wikipedia_en_all_nopic_01_2012/I/f8be82a938f8c47805cfac76179ed409.png)
In the case of the fifth root of 34 above (after dividing out common factors):
![\sqrt[5]{34} = 2%2B\cfrac{1} {40%2B\cfrac{4} {4%2B\cfrac{6} {120%2B\cfrac{9} {4%2B\cfrac{11} {200%2B\cfrac{14} {4%2B\ddots}}}}}}
=2%2B\cfrac{4\cdot 1}{165-1-\cfrac{4\cdot 6}{495-\cfrac{9\cdot 11}{825-\cfrac{14\cdot 16}{1155-\ddots}}}}.](/2012-wikipedia_en_all_nopic_01_2012/I/6a08ca7bbb4404976826f57d81c015a5.png)
Complex roots
Every complex number other than 0 has n different nth roots.
Square roots
The two square roots of a complex number are always negatives of each other. For example, the square roots of −4 are 2i and −2i, and the square roots of i are
If we express a complex number in polar form, then the square root can be obtained by taking the square root of the radius and halving the angle:
A principal root of a complex number may be chosen in various ways, for example
which introduces a branch cut in the complex plane along the positive real axis with the condition 0 ≤ θ < 2π, and along the negative real axis with −π < θ ≤ π.
Roots of unity
The number 1 has n different nth roots in the complex plane, namely
where
These roots are evenly spaced around the unit circle in the complex plane, at angles which are multiples of  . For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1,
. For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1,  , −1, and
, −1, and 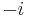 .
.
nth roots
Every complex number has n different nth roots in the complex plane. These are
where η is a single nth root, and 1, ω, ω2, ... ωn−1 are the nth roots of unity. For example, the four different fourth roots of 2 are
In polar form, a single nth root may be found by the formula
As with square roots, the formula above cannot be applied consistently to the entire complex plane, but instead leads to a branch cut at the points where θ / n suddenly “jumps”.
Solving polynomials
It was once believed that all roots of polynomials could be expressed in terms of radicals and elementary operations; however, the Abel-Ruffini theorem (1824) shows that this is not true in general. For example, the solutions of the equation
cannot be expressed in terms of radicals. (cf. quintic equation)
For solving any equation of the nth degree numerically, see Root-finding algorithm.
See also
- Nth root algorithm
- Shifting nth-root algorithm
- Irrational number
- Algebraic number
- Nested radical
- Twelfth root of two
- Super-root
References
- ^ Bansal, R K (2006). New Approach to CBSE Mathematics IX. Laxmi Publications. p. 25. ISBN 9788131800133. http://books.google.com/books?id=1C4iQNUWLBwC&pg=PA25#v=onepage&q&f=false.
- ^ Silver, Howard A. (1986). Algebra and trigonometry. Englewood Cliffs, N.J.: Prentice-Hall. ISBN 0130212709.
- ^ Leonhard Euler (1755) (in Latin). Institutiones calculi differentialis.
- ^ "Earliest Known Uses of Some of the Words of Mathematics". Mathematics Pages by Jeff Miller. http://jeff560.tripod.com/s.html. Retrieved 2008-11-30.
- ^ McKeague, Charles P. (2011). Elementary algebra. p. 470. http://books.google.com/books?id=etTbP0rItQ4C&printsec=frontcover&dq=editions:q0hGn6PkOxsC&hl=sv&ei=52CsTqv9Go7sOZ_tldAP&sa=X&oi=book_result&ct=result&resnum=2&ved=0CDEQ6AEwAQ#v=onepage&q&f=false.

![\sqrt[n]{x} \,=\, x^{1/n}](/2012-wikipedia_en_all_nopic_01_2012/I/f6e2875466bdf9e5eb4a7db071b8e812.png)
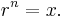

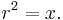
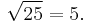
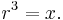
![\sqrt[3]{8}\,=\,2\quad\text{and}\quad\sqrt[3]{-8}\,= -2.](/2012-wikipedia_en_all_nopic_01_2012/I/9a3f9a68113114bb84da1c3e1c0e1e48.png)
![\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b} \,,](/2012-wikipedia_en_all_nopic_01_2012/I/1c4a72da0039879d6a3f51c2a3cd7842.png)
![\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \,.](/2012-wikipedia_en_all_nopic_01_2012/I/bda2aa437b256dd2810e496f88cd0cbe.png)
![\sqrt[n]{a^m} = \left(a^m\right)^{\frac{1}{n}} = a^{\frac{m}{n}}.](/2012-wikipedia_en_all_nopic_01_2012/I/fa8470504bf32778b14907106851fbae.png)

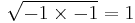
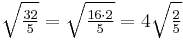


![\frac{1}{\sqrt[3]{a}%2B\sqrt[3]{b}} = \frac{\sqrt[3]{a^2}-\sqrt[3]{ab}%2B\sqrt[3]{b^2}}{(\sqrt[3]{a}%2B\sqrt[3]{b})(\sqrt[3]{a^2}-\sqrt[3]{ab}%2B\sqrt[3]{b^2})} = \frac{\sqrt[3]{a^2}-\sqrt[3]{ab}%2B\sqrt[3]{b^2}}{a%2Bb} \,.](/2012-wikipedia_en_all_nopic_01_2012/I/7c0451ee16e40408d714290ff68a3bc2.png)
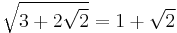

![\sqrt[5]{34} = 2.024397458 \ldots.](/2012-wikipedia_en_all_nopic_01_2012/I/91d88869e29ad05e687ded2320e27182.png)
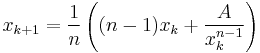
![\sqrt[n]{x^n%2By} \approx x %2B \frac{y}{n x^{n-1}}.](/2012-wikipedia_en_all_nopic_01_2012/I/a25d581b7161170fc8ab0dbe74532ecc.png)
![\sqrt[5]{34} = \sqrt[5]{32 %2B 2} \approx 2 %2B \frac{2}{5 \cdot 16} = 2.025.](/2012-wikipedia_en_all_nopic_01_2012/I/198ae9a2e87d4552f51a383d13d46598.png)
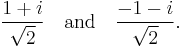
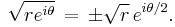
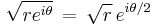
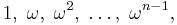

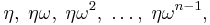
![\sqrt[4]{2},\quad i\sqrt[4]{2},\quad -\sqrt[4]{2},\quad\text{and}\quad -i\sqrt[4]{2}.](/2012-wikipedia_en_all_nopic_01_2012/I/9694f35fef8ad7c207131fcb2770c6dd.png)
![\sqrt[n]{re^{i\theta}} \,=\, \sqrt[n]{r}\,e^{i\theta/n}.](/2012-wikipedia_en_all_nopic_01_2012/I/9a363b547d8719bf4f2a7f2da0f504e5.png)
